在R语言中,函数用于执行一个或两个样本的t检验(t-test)。t检验是一种常用的统计方法,用于比较两个样本的均值是否有显著差异。
其输出结果具有属性值,用$调用对象属性!
t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95)
参数说明:
-
x:第一个样本数据,可以是数值向量或数值型的数据框。 -
y:第二个样本数据,同样可以是数值向量或数值型的数据框。如果只有一个样本,可以省略此参数。 -
alternative:指定检验的双侧("two.sided")、单侧小于("less")还是单侧大于("greater")的假设检验,默认为"two.sided"。
two.sided:双侧检验,备用假设不等于μ0;
less:左侧检验,备择假设小于mu(μ0);双样本中指第一个样本的均值是否小于第二个样本的均值;
greater:右侧检验,备择假设大于mu(μ0);双样本中指第一个样本的均值是否大于第二个样本的均值;
-
mu:要检验的均值差异是否与给定值mu有显著差异,默认为0,即检验均值是否相等。 给定值可以理解为总体均值μ; 两个样本下mu为0,检验均值是否相等? -
paired:一个逻辑值,指示是否进行配对样本的t检验,默认为FALSE。如果为TRUE,则表示进行配对样本的t检验。 是否进行配对t检验(paired t-test),跟双样本t检验不同! -
var.equal:一个逻辑值,指示是否假设两个样本的方差相等,默认为FALSE。如果为TRUE,则表示假设方差相等。
TRUE,student's t-test 两个样本满足方差齐性,方差基本一致
FALSE,welch's t-test(韦尔奇t检验) 两个样本不满足方差齐性,方差不整奇,方差差异较大
conf.level:置信水平,默认为0.95,表示计算95%的置信区间。
函数功能:根据提供的样本数据执行t检验,并返回检验结果,包括t统计量、p值和置信区间。
以下是一个示例,演示如何使用t.test()函数执行t检验:
# 执行一个样本的t检验
data <- c(5, 7, 6, 8, 4, 9, 5, 6)
t.test(data, mu = 6)
# 执行两个独立样本的t检验
group1 <- c(5, 7, 6, 8, 4)
group2 <- c(9, 5, 6, 7, 5)
t.test(group1, group2)
data执行了一个样本的t检验,检验是否存在与均值6不同的显著差异。然后,我们使用两个独立的样本数据group1和group2执行了两个样本的独立t检验,检验两个样本的均值是否有显著差异。
通过t.test()函数,我们可以获取关于检验结果的详细信息,如t统计量、p值和置信区间。根据检验结果,我们可以判断样本之间的均值差异是否显著。
关于t.test的结果list中的参数选取¶
t.test换回的结果是列表结构!
One Sample t-test
data: data_q4$age
t = 152, df = 409, p-value <2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
30 31
sample estimates:
mean of x
30
t.test()函数返回的结果列表的组成内容如下: 1. statistic:统计量的值,例如t值、z值等。 2. parameter:自由度,即用于计算统计量的参与观测值的数量。 3. p.value:双侧检验的p值。 4. conf.int:置信区间的上下限值。
t.test(data_q4$age)[4](4)
# 或
t.test(data_q4$age)$conf.int
# 输出
[1] 30 31
attr(,"conf.level")
[1] 0.95
单样本t检验¶
双边t检验¶
样本是王老师班级的学生成绩,mu是全校总体成绩的均值为137。
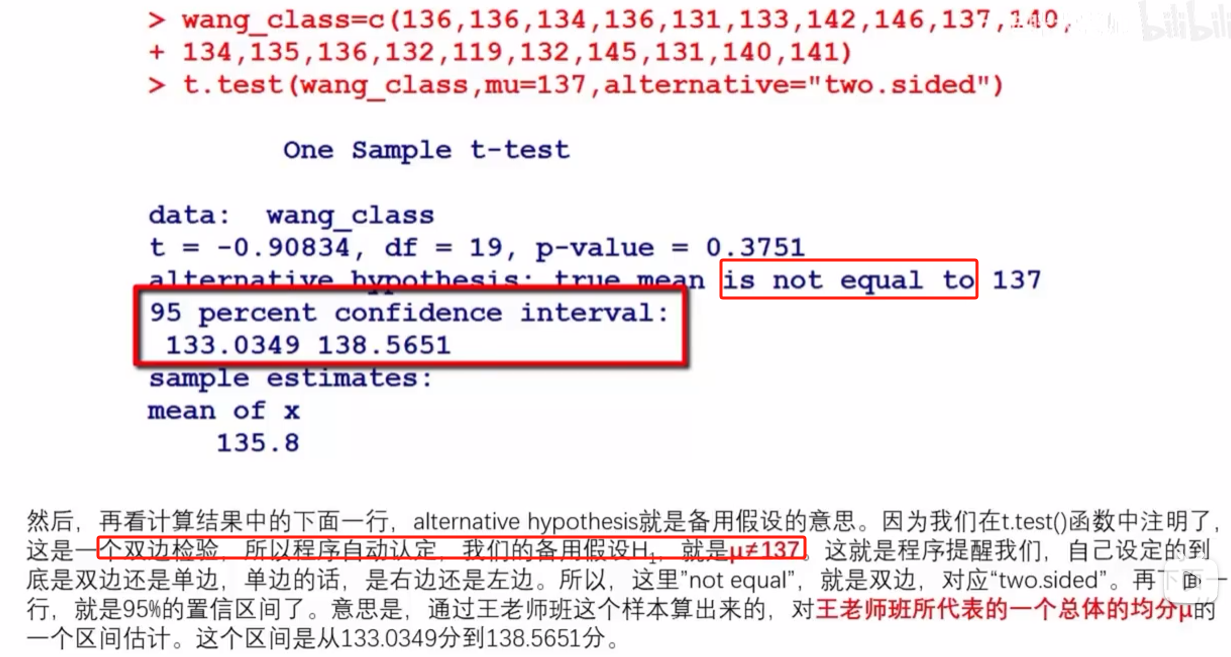
1,从t分布的角度: t-value:指的是一侧的t值; p-value:两侧加起来的p值,t=-0.908,对应的qt(-0.908, df=19)为0.1876。
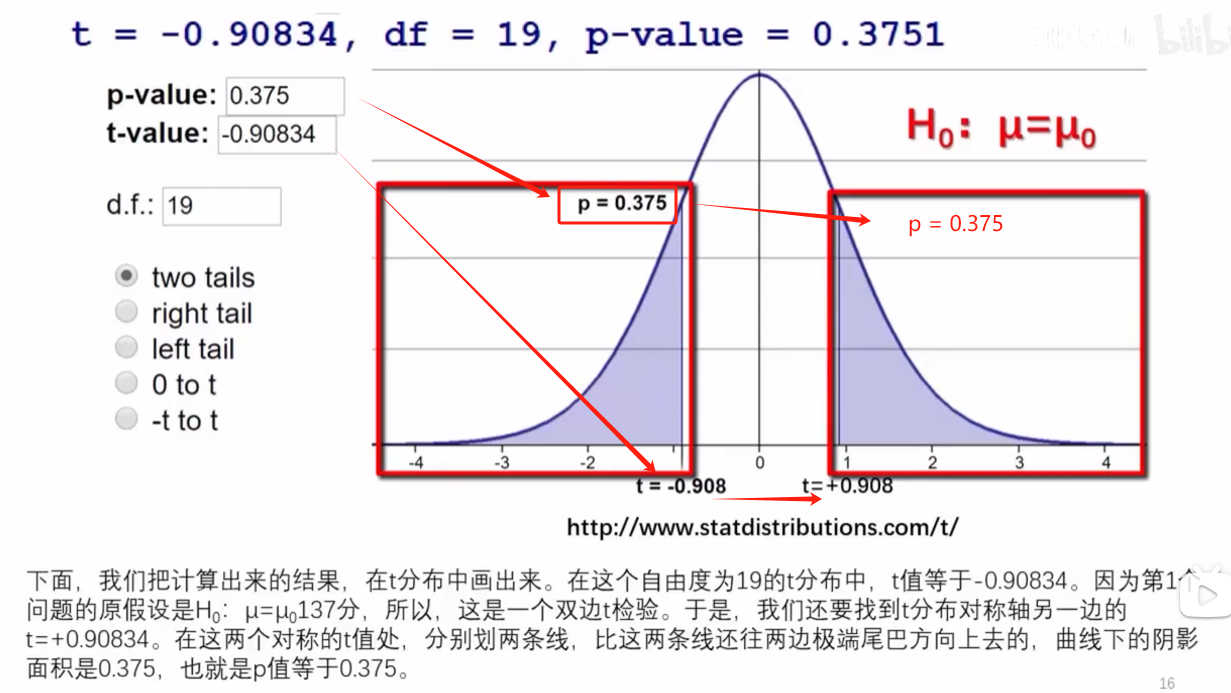
2,从样本均值分布的角度: 置信度为95%的置信区间: 样本均值x_bar为135.80:为这个样本容量为20的样本的均值;置信区间指的是样本均值分布上的区间!而非总体分布上的区间
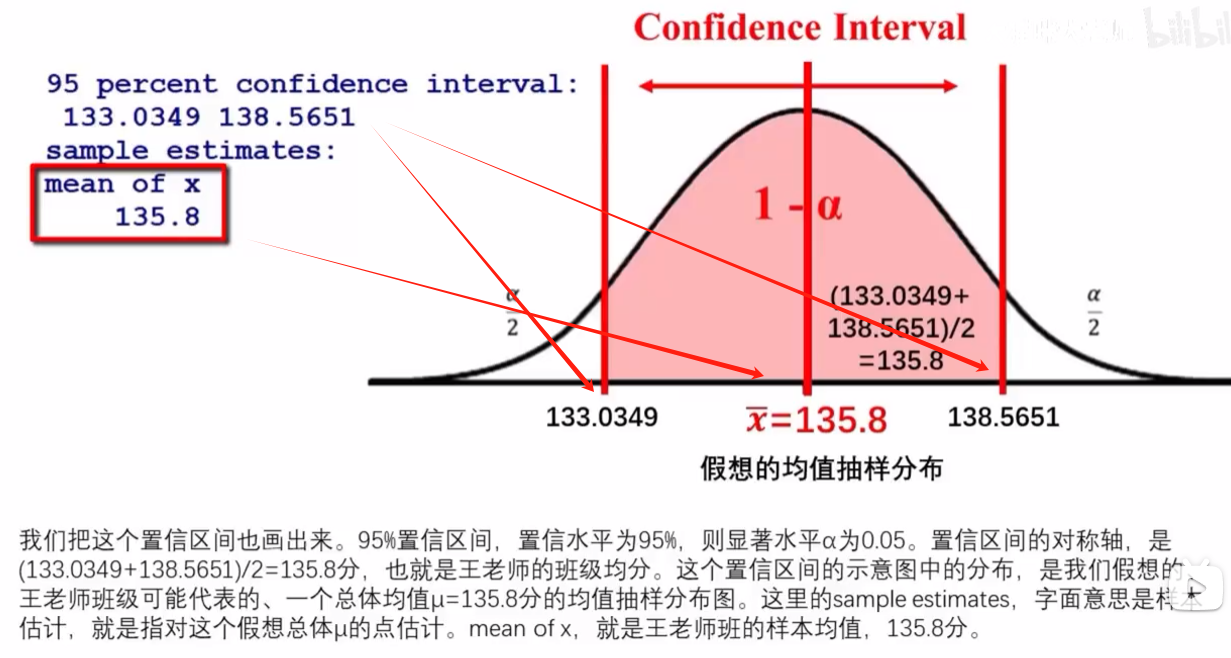
结论¶
1,看t值,对比的是自由度一样的t分布
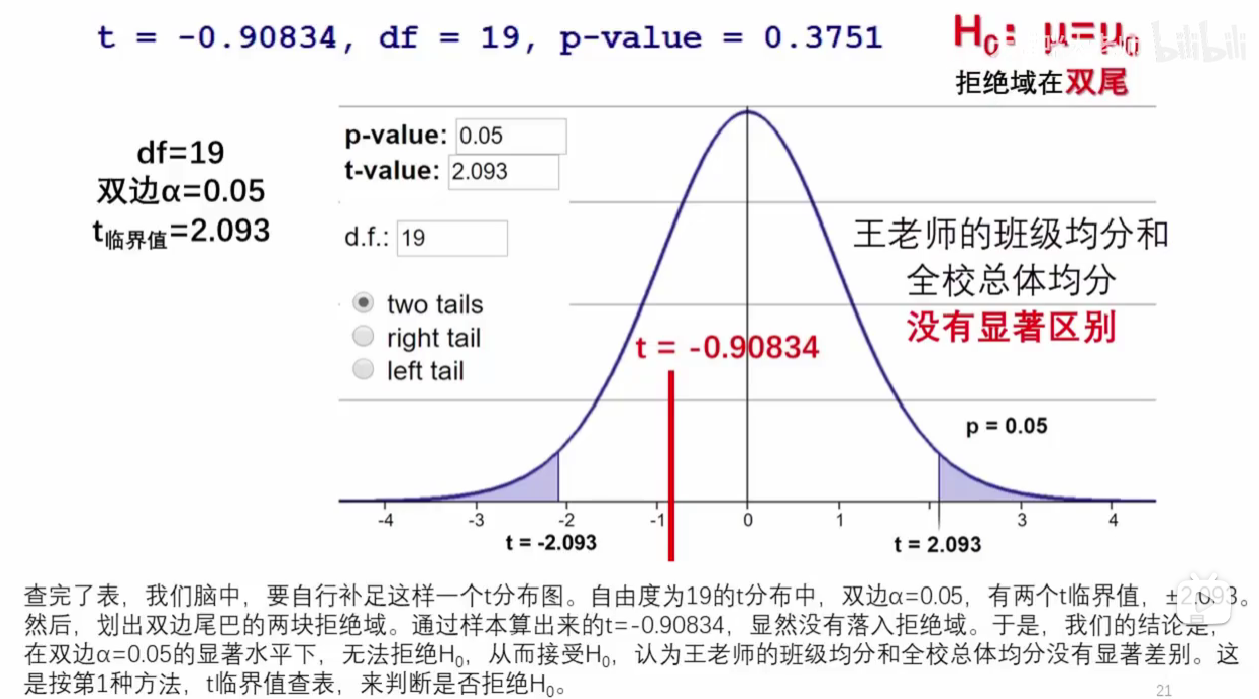
2,看p值:为左右两侧的和值

3,看置信区间是否包含μ0,就是上面的mu值

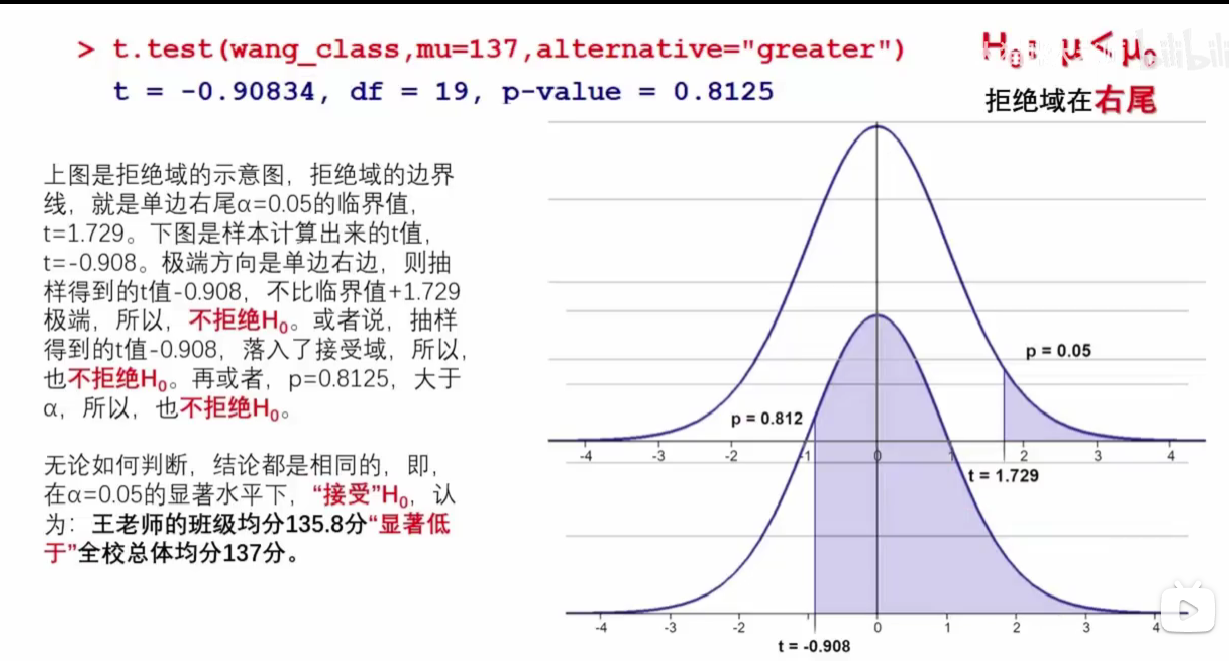
单边t检验:右侧假设检验¶
备择假设H_1为μ>μ0

t-value、p-value、置信区间的参数理解类似双侧。
结论¶
1,t值=-0.908<1.729(α对应的t值),拒绝备择假设H_1,假设检验的有效性体现在备择假设(犯错误的概率α)上。H_0的选择具有主观性,更难证伪;
2,p值=0.8125>α=0.05,拒绝备择假设;
3,置信区间[133.5157, inf),μ0=137,被包含在内,拒绝备择假设H_1。 跟“接受域”相区分,置信区间是从样本均值分布的角度上看的,取值依托于本次样本均值x_bar和选择的α,此处\(133.5157=\color{red}{\overline{x}-t*\frac s{\sqrt n}}\);接受域也是从样本均值分布的角度上看的,只是依托于μ(总体均值,根据大数定律,也是样本均值分布的均值)和选择的α。
(图中只显示了t分布中的t、p值,置信区间的下边界在样本均值分布中的x_bar=135.8的左侧)
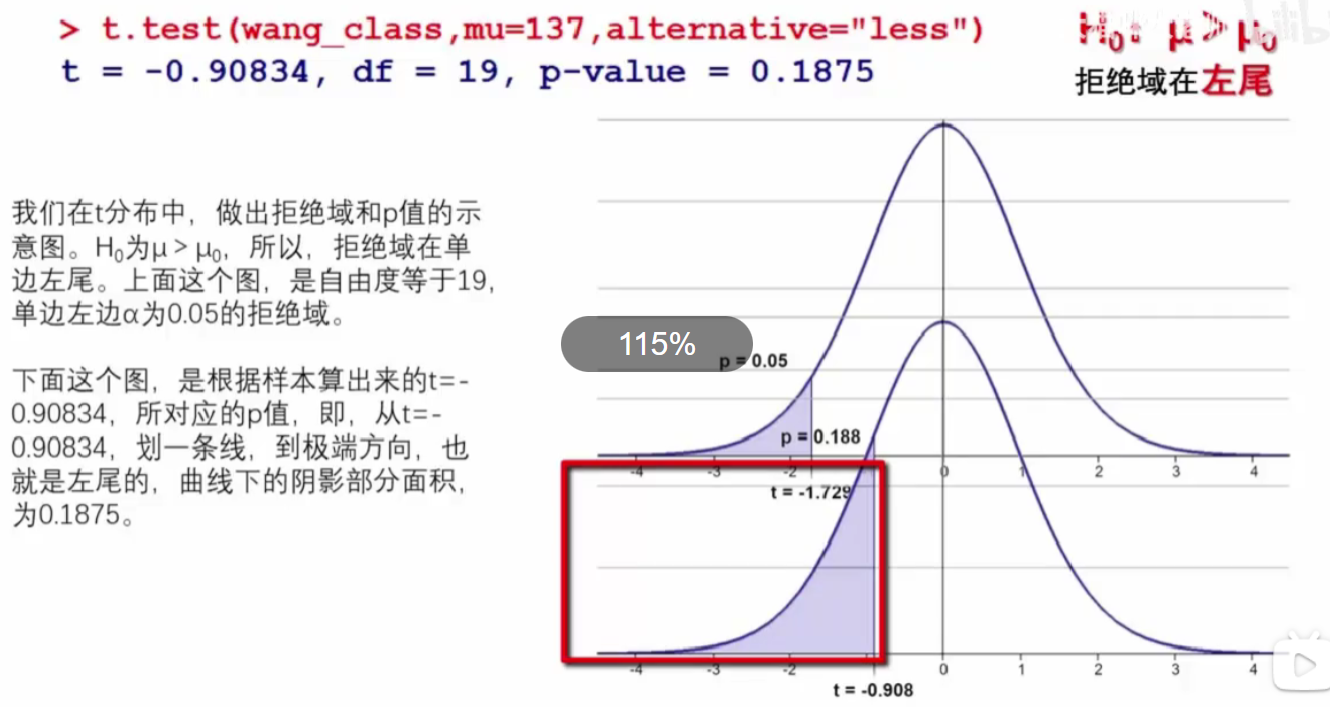
单边t检验:左侧假设性检验¶
备择假设H_1为μ<μ0

library(tidyverse)
wang_class=c(136,136,134,136,131,133,142,146,137,140,134,135,136,132,119,132,145,131,140,141)
t.test(wang_class ,mu=137,alternative="greater")
结论¶
1,t值=-0.908>-1.729(α对应的t值),拒绝备择假设H_1;
2,p值=0.188>α=0.05,拒绝备择假设;
3,置信区间(-inf, 138.0843],\(138.0843=\color{red}{\overline{x}+t*\frac s{\sqrt n}}\),μ0=137没被包含在内,接受备择假设H_1。
(图中只显示了t分布的t、p值,置信区间的上边界在样本均值分布中的x_bar=135.8的右侧)
双样本t检验¶
独立样本t检验¶
双样本双边t检验¶
双样本单边t检验¶
配对样本t检验¶
(数据是d值,实质是单样本假设检验。) 备择假设H_1:后侧大于前测成绩(等价于单样本中x_bar大于0,单样本右侧检验)
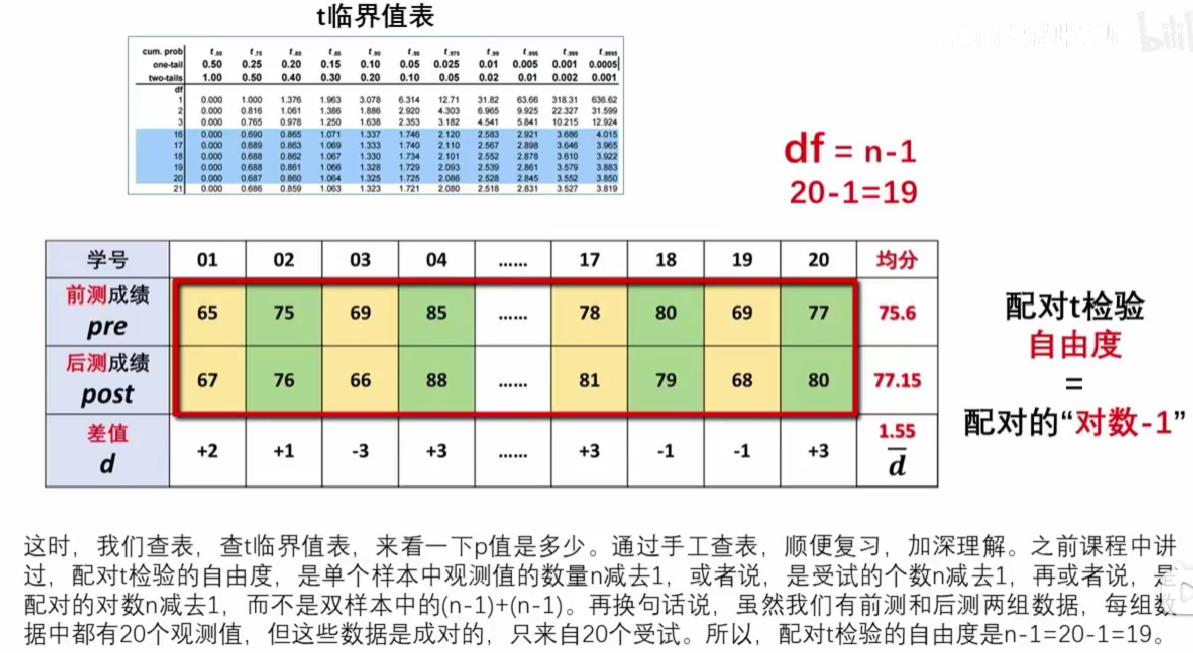
post:后测成绩;
pre:前侧成绩,相当于上面的mu;
paired=TRUE;
greater:备择假设后侧大于前侧成绩;
df=19,算法自动计算。
